最新の理論を考察。
円運動（公転軌道）から導かれる新たな卓球理論　「シャカシャカ理論」を展開

初心者や、中高年を対象に画期的な打法を「すりゴマ打法」を開発しました。

中高年のための卓球講座としてその一部を公開しました。

これから卓球をはじめたい。 基本を一から学びたい。 足腰の筋力が衰え、若い時のように動けない。 肩、腕、腰の疲労からくる痛みが取れない。 動体視力が低下、スピードについていけない。

シャカシャカ理論で解決!!

☑動かないで打球 ☑ランダムが最大の武器 ☑攻めはゆっくり、守りは早く ☑コートの2/3はバックで処理 ☑台との距離を知る ☑ネットインが取れなければ、いつまでも初心者 ☑レシーブから攻める

シャカシャカ理論の概要

●新たな卓球理論 ●シャカシャカ理論 ●すりゴマ打法とは　・フォアーハンド 　シェークハンド／ペンホルダー　・バックハンド　シェークハンド／ペンホルダー 　●実践編 ●まとめ

ＩＮＤＥＸ

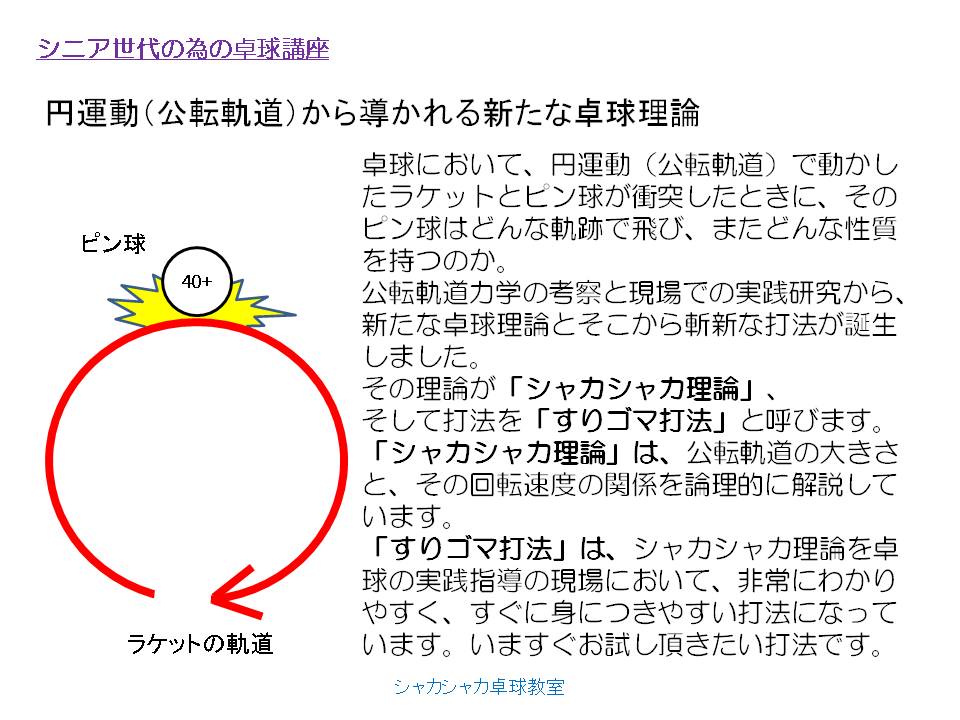
卓球において、円運動（公転軌道）で動かしたラケットとピン球が衝突したときに、そのピン球はどんな軌跡で飛び、またどんな性質を持つのか。 公転軌道力学の考察と現場での実践研究から、新たな卓球理論とそこから斬新な打法が誕生しました。 その理論が「シャカシャカ理論」、 そして打法を「すりゴマ打法」と呼びます。 「シャカシャカ理論」は、公転軌道の大きさと、その回転速度の関係を論理的に解説しています。 「すりゴマ打法」は、シャカシャカ理論を卓球の実践指導の現場において、非常にわかりやすく、すぐに身につきやすい打法になっています。いますぐお試し頂きたい打法です。

シニア世代の為の卓球講座-円運動（公転軌道）から導かれる新たな卓球理論

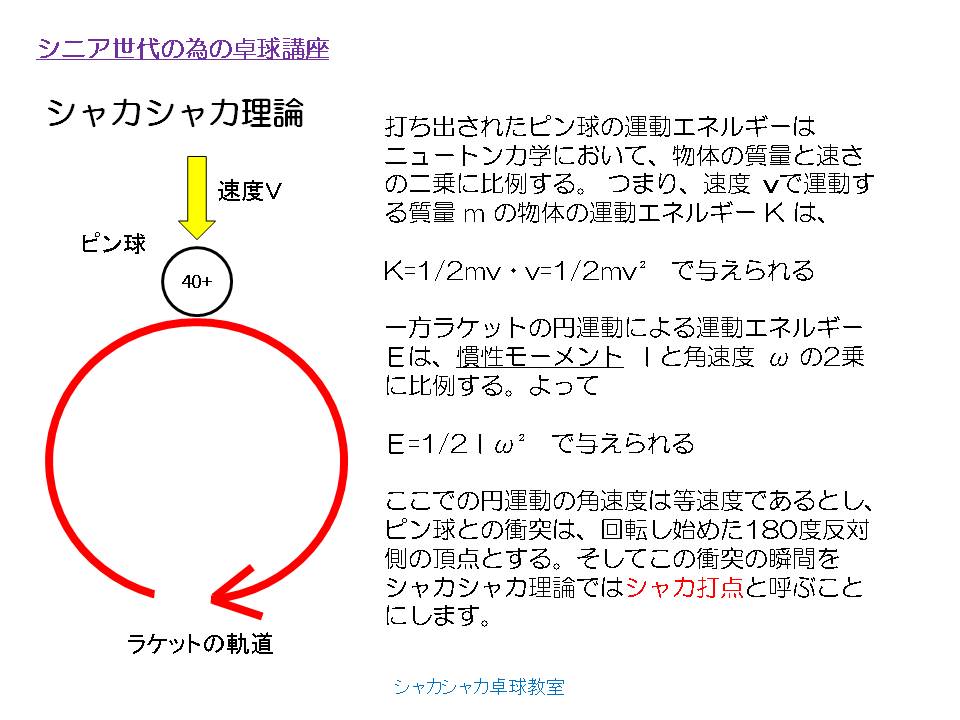
打ち出されたピン球の運動エネルギーはニュートン力学において、物体の質量と速さの二乗に比例する。 つまり、速度 vで運動する質量 m の物体の運動エネルギー K は、 K=1/2mv・v=1/2mv²　で与えられる 一方ラケットの円運動による運動エネルギーＥは、慣性モーメント Ｉと角速度 ω の2乗に比例する。よって Ｅ=1/2Ｉω²　で与えられる ここでの円運動の角速度は等速度であるとし、ピン球との衝突は、回転し始めた180度反対側の頂点とする。そしてこの衝突の瞬間をシャカシャカ理論ではシャカ打点と呼ぶことにします。

シニア世代の為の卓球講座-シャカシャカ理論

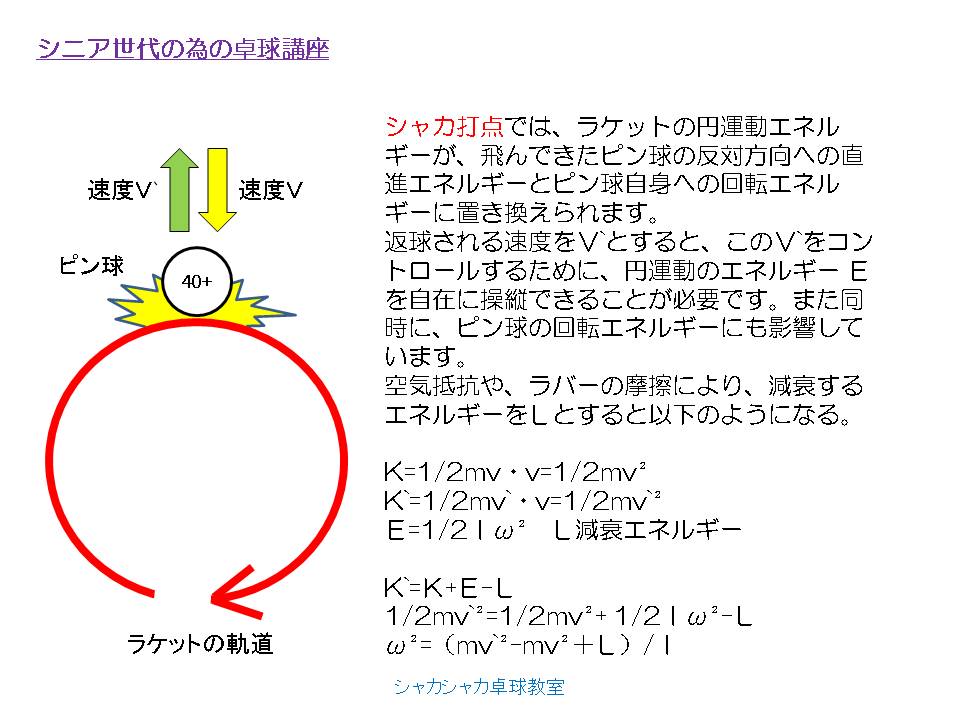
シャカ打点では、ラケットの円運動エネルギーが、飛んできたピン球の反対方向への直進エネルギーとピン球自身への回転エネルギーに置き換えられます。 返球される速度をＶ`とすると、このＶ`をコントロールするために、円運動のエネルギー Ｅを自在に操縦できることが必要です。また同時に、ピン球の回転エネルギーにも影響しています。 空気抵抗や、ラバーの摩擦により、減衰するエネルギーをＬとすると以下のようになる。 K=1/2mv・v=1/2mv² K`=1/2mv`・v=1/2mv`² Ｅ=1/2Ｉω²　Ｌ減衰エネルギー K`=Ｋ+Ｅ-Ｌ 1/2mv`²=1/2mv²+ 1/2Ｉω²-Ｌ ω²=（mv`²-mv²＋Ｌ）/Ｉ

シニア世代の為の卓球講座-シャカ打点

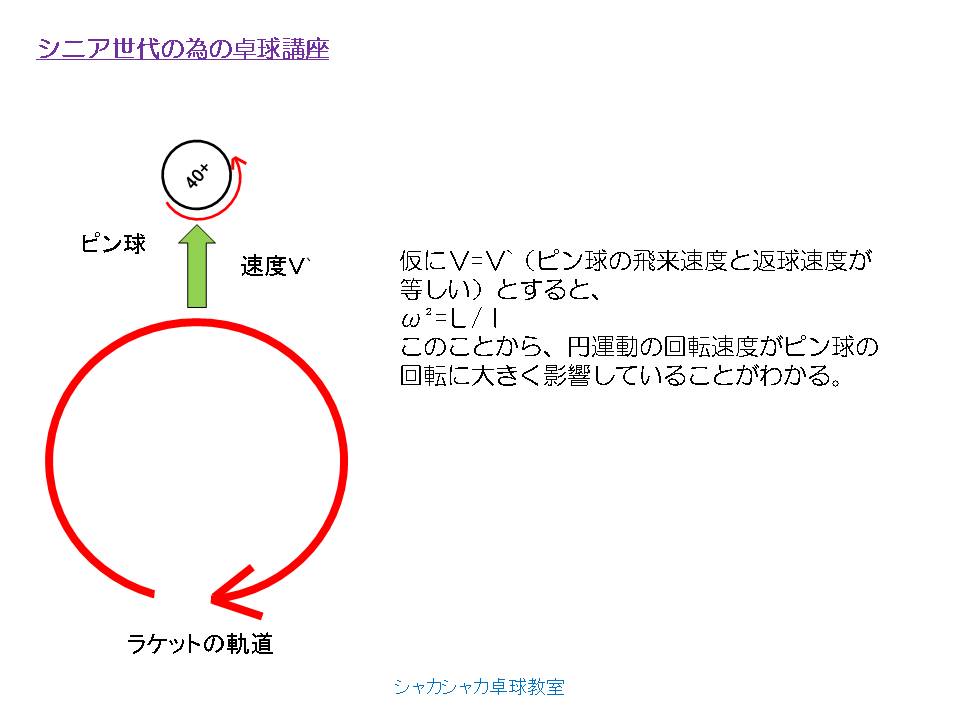
仮にＶ=Ｖ`（ピン球の飛来速度と返球速度が等しい）とすると、 ω²=Ｌ/Ｉ このことから、円運動の回転速度がピン球の回転に大きく影響していることがわかる。

シニア世代の為の卓球講座-シャカ打点2

次に、ラケット軌道の円の大きさの違いによるピン球への影響を考察します。 円運動エネルギーＫは、回転速度（角速度ω）が同じであるならば、 Ｋ=1/2Ｉω²であることから、ラケット軌道の大きさの違いによる影響は、 慣性モーメントＩに比例する。すなわち軌道の半径の大きさが、ピン球の速度と回転に影響することになる。 影響の度合いは、今後の実践で検証していく。

シニア世代の為の卓球講座-ラケット軌道の円の大きさの違いによるピン球への影響

特長-①円運動を基本にしているので、打ち終えたらもと姿勢に戻っている。 ②ボールの上下の回転の影響を受けにくいので、同じフォームでいろいろな回転のボールを打つ事ができる。 ③フォアーハンド、バックハンドとも同じ様に適応できる。 ④スピードは、円の大きさと、円運動のスピードで調整できる。 ⑤自然な直立姿勢で、足腰に負担がかからない。 ⑥シンプルな動作のため、打球動作が崩れない。

シニア世代の為の卓球講座-擦りゴマ打法

卓球レッスンについてはこちらで詳しくはお問い合わせください。